March 24, 2025
In this post, I talk about a course I just finished teaching at École Polytechnique on scientific machine learning.
Introduction
The course was aimed at third-year students at École Polytechnique, who had completed two years of classes préparatoires, making the material equivalent to a graduate-level course in the UK or US. This Scientific Machine Learning (SciML) course bridged the gap between Scientific Computing and Machine Learning. SciML, an emerging field, enables efficient methods for solving complex problems in science and engineering, like partial differential equations (PDEs). This course offered a new, valuable specialization, helping students stand out in the evolving job market, where demand for ML experts with specialized skills is growing.
Scientific computing and numerical analysis
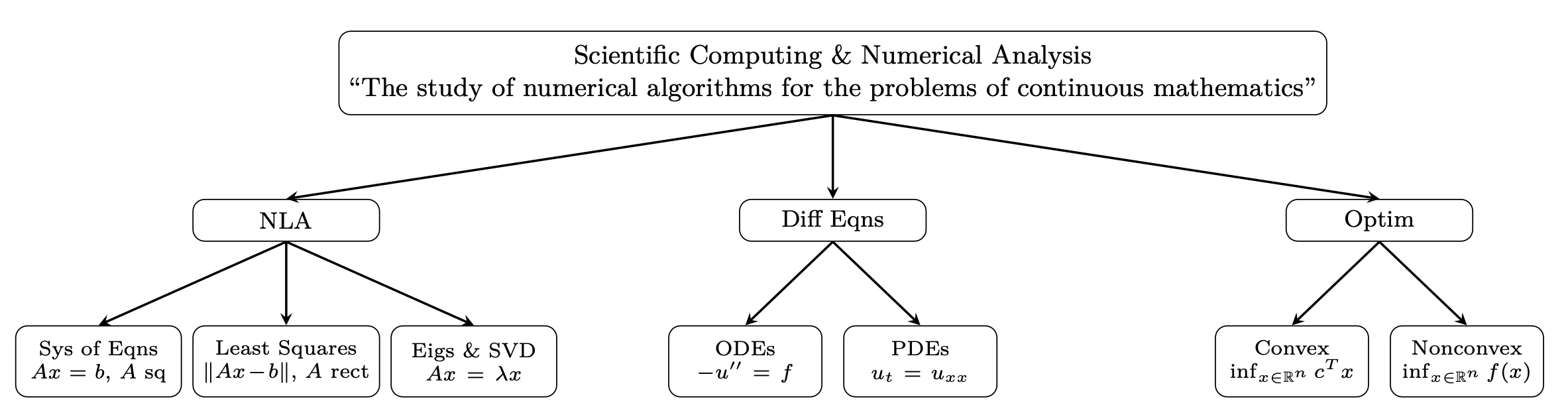
Scientific Computing and Numerical Analysis are branches of applied mathematics that focus on the development and analysis of numerical algorithms for solving problems in continuous mathematics, such as PDEs.
When a PDE is linear, we first discretize it on a grid or mesh and then solve it using linear algebra. This creates a natural connection between PDEs and Numerical Linear Algebra (NLA).
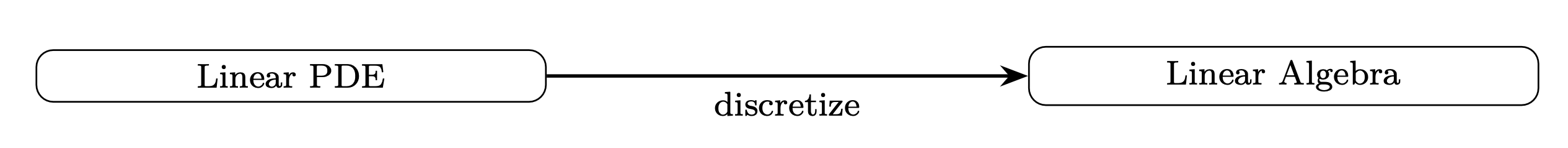
Sometimes, when an energy functional exists for a problem (e.g., PDEs with coercive bilinear forms like the Laplace equation), we can also apply optimization techniques to solve it effectively.
A typical approach to solving nonlinear PDEs involves transforming the problem into a sequence of linear problems, through linearization and iteration. In this way, nonlinear PDEs are reduced to linear algebra problems.

Scientific machine learning
SciML is a recent research field based on both machine learning and scientific computing. Its goal is the development of robust, efficient, and interpretable methods to solve problems in science and engineering, such as PDEs, parameter identification, or inverse problems.
In SciML, a common approach to solving nonlinear PDEs starts with generating training data, typically using standard numerical solvers, where the training data consists of reference solutions. This data is then used to construct a cost function that quantifies the training error, while the solution or solution operator is discretized using a neural network. The goal is to minimize this cost function through optimization to learn the optimal network weights.

This brings optimization back to the core of the numerical solutions of PDEs.
Overview
Throughout the course, we touched upon all major fields of Scientific Computing and Numerical Analysis, including Numerical Linear Algebra, PDEs, and Optimization, with a ML flavor. Each method discussed was implemented in Python, and every tutorial provided hands-on experience through notebooks. This ensured that students not only understood the theoretical aspects but also gained practical experience in implementing and using these methods. Check out my lecture notes!
- Supervised Learning
- Chapter 1 — Supervised Learning without Neural Networks
- Linear and nonlinear least squares with QR and Gauss Newton's method
- Trigonometric interpolation with the FFT
- Chapter 2 — Supervised Learning with Neural Networks
- Artificial neural networks
- Training with stochastic gradient descent and backpropagation
- Chapter 3 — Neural Network Approximation Theory
- Universality theorems
- Quantitative estimates in Sobolev spaces
- Chapter 1 — Supervised Learning without Neural Networks
- Solving PDEs
- Chapter 4 — Solving PDEs without Neural Networks
- Finite elements for the 1D Poisson equation
- Finite elements with finite differences for the 1D heat equation
- Chapter 5 — Solving PDEs with Neural Networks
- Physics-informed neural networks
- Chapter 6 — Solving PDEs with Neural Networks 2 (Samuel Kokh)
- Chapter 4 — Solving PDEs without Neural Networks
- Solving Parametric PDEs
- Chapter 7 — Solving Parametric PDEs without Neural Networks
- Reduced basis methods with the SVD
- Chapter 8 — Solving Parametric PDEs with Neural Networks
- Deep operator networks
- Fourier neural operators
- Chapter 7 — Solving Parametric PDEs without Neural Networks