Bonjour—

Welcome to the seventh and last entry in my Holiday in Sicily series. Here we are. The full eruption. It’s no coincidence I’m writing this from Sicily, flying back over Etna’s crater. I call it Mafia, and I’m a quarter Italian, so I get a pass. But this isn’t a vendetta; it’s a reflection. And yes, I love my lab, I love my job, and I know how incredibly privileged I am. Tenure with no grant pressure, no publishing quotas. Most researchers land a permanent job after one or two postdocs. Then you’re a civil servant—and short of criminal activity, you can never be fired. Sounds amazing, right?

Welcome to the sixth and penultimate entry in my Holiday in Sicily series. Coincidentally, as I write this, Etna is erupting, just in time for today’s post, where I finally turn to the main volcano: the French academic and meritocratic system. The one I approached two posts ago, and which is now showing signs of violent activity. The magma chamber is fracturing. The smoke is rising. The eruption has begun.

Welcome to the fifth entry in my Holiday in Sicily series. As I sip a strong espresso under the Etna sun, I can’t help but feel it: the eruption is getting closer. Not just from Etna—though it’s rumbling again—but from the growing volcano in computational science. I’m talking about Scientific Machine Learning (SciML) and its most explosive crater: Physics-Informed Neural Networks (PINNs).

Welcome to the fourth entry in my Holiday in Sicily series. Starting with this post—and even more so in the next few—my opinions will become progressively more controversial. Call it the mathematical equivalent of hiking closer to Mount Etna: things might get heated, and by blog seven, expect a full eruption. Today, I reflect on the influence of Bourbaki on French mathematics, and the tension between rigor and intuition in how we learn, teach, and research.

Welcome to the third entry in my Holiday in Sicily series. Today’s reflection comes from a quiet morning walk in Taormina. It got me thinking about how researchers choose between digging deeper into old, technical questions and venturing out into broad, unfamiliar territory. Both paths have their charm—and their challenges.

Welcome to the second entry in my Holiday in Sicily series. Today, I reflect on the interplay between algorithms and theory—how practice often leads, theory follows, and how the two shape each other in a dynamic loop that drives much of applied math progress.

Welcome to the first entry in my Holiday in Sicily series. Over the next 13 days, while vacationing in Sicily, I’ll be posting here every other day. In today’s post, I reflect on the practice of writing research memos—why I do it, how it helps, and how surprisingly enjoyable the process can be.

In this post, I talk about a course I just finished teaching at École Polytechnique on scientific machine learning.

In this post, I talk about an extension of the linear sampling method (LSM) for solving the sound-soft inverse acoustic scattering problem with data generated by randomly distributed small scatterers. For details, check out my paper with Houssem Haddar and Josselin Garnier!

In this post, I talk about a new method for computing strongly singular and near-singular integrals that arise when solving the 3D Helmholtz equation with curved boundary elements.

In this post, I talk about coupling the finite and boundary element methods for solving wave propagation problems in an inhomogeneous medium.

In this post, I talk about image and video matting—the process of extracting specific objects from an image to place them in a scene of a movie or compose them onto another background.

In this post, I talk about an extension of the linear sampling method (LSM) for solving the sound-soft inverse acoustic scattering problem with randomly distributed point sources. For details, check out my paper with Houssem Haddar and Josselin Garnier!

In this post, I talk about a new method for computing weakly singular and near-singular integrals that arise when solving the 3D Helmholtz equation with curved boundary elements.

In this post, I talk about quantum computing for supervised learning. Marcello Benedetti and his colleagues wrote a very nice review last year, which I highly recommend.

In this post, I talk about quantum computing for solving nonlinear ordinary differential equations (ODEs). In a recent paper, Michael Lubasch and his colleagues proposed an algorithm to solve such equations using a combination of classical and quantum computers.

Episode 2 of my series on quantum computing—in this post, I talk about the Schrödinger equation and quantum logic gates, which are the building blocks of quantum circuits and quantum computers.

In my first research project as an undergraduate student in the summer of 2010, I worked on groups and symmetries in classical and quantum physics. One day in the library I came across Noether's theorem, which links symmetries (e.g., time invariance) to conserved quantities (e.g., energy). Noether was one of the leading mathematicians of her time and made major contributions to both algebra and mathematical physics. Learning about her work was a decisive moment in my life because I realized for the first time how deeply connected mathematics and physics were.

Depuis mon retour en France, un sujet de conversation récurrent est bien évidemment la pandémie de la Covid-19. Et là, grosse surprise : beaucoup de gens autour de moi pensent toujours que l'hydroxychloroquine est, ou pourrait être, un médicament efficace contre la Covid-19. Ce qui est surprenant, c'est qu'aux États-Unis, la folie derrière l'hydroxychloroquine est terminée ! Mais pas en France.

One of the papers I wrote during my Ph.D. at Oxford with Niall Bootland was just accepted in Mathematics and Computers in Simulation. In this post, I review the main ideas of the paper.

I've been paying careful attention to the various government policies implemented in response to the coronavirus pandemic. Having many friends and colleagues in the U.K., I am particularly concerned with the British government's plan of action.

In my latest paper, my colleague and I prove a theorem about the approximation of multivariate functions by deep ReLU networks, for which the curse of dimensionality is lessened. Our theorem is based on a constructive proof of the Kolmogorov–Arnold superposition theorem, and on a subset of multivariate continuous functions whose outer superposition functions can be efficiently approximated by deep ReLU networks.

In a recent paper, my colleagues and I considered the deep ReLU network approximation of generalized bandlimited functions \(f:B=[0,1]^d\rightarrow\mathbb{R}\) of the form $$ f(\boldsymbol{x}) = \int_{\mathbb{R}^d}F(\boldsymbol{w})K(\boldsymbol{w}\cdot\boldsymbol{x})d\boldsymbol{w}, $$ with \(\mathrm{supp}\,F\subset[-M,M]^d\), \(M\geq1\), and for some square-integrable function \(F:[-M,M]^d\rightarrow\mathbb{C}\) and analytic \(K:\mathbb{R}\rightarrow\mathbb{C}\). We showed that, for any measure \(\mu\), such functions can be approximated with error \(\epsilon\) in the \(L^2(B,\mu)\)-norm by deep ReLU networks of depth \(L=\mathcal{O}\left(\log_2^2\frac{1}{\epsilon}\right)\) and size \(W=\mathcal{O}\left(\frac{1}{\epsilon^2}\log_2^2\frac{1}{\epsilon}\right)\), up to some constants that depend on \(F\), \(K\), \(\mu\) and \(B\).

A couple of weeks ago, I spent a few days at McGill University with Jean-Philippe Lessard. He introduced me to the world of computer-assisted proofs, which I briefly describe in this post.

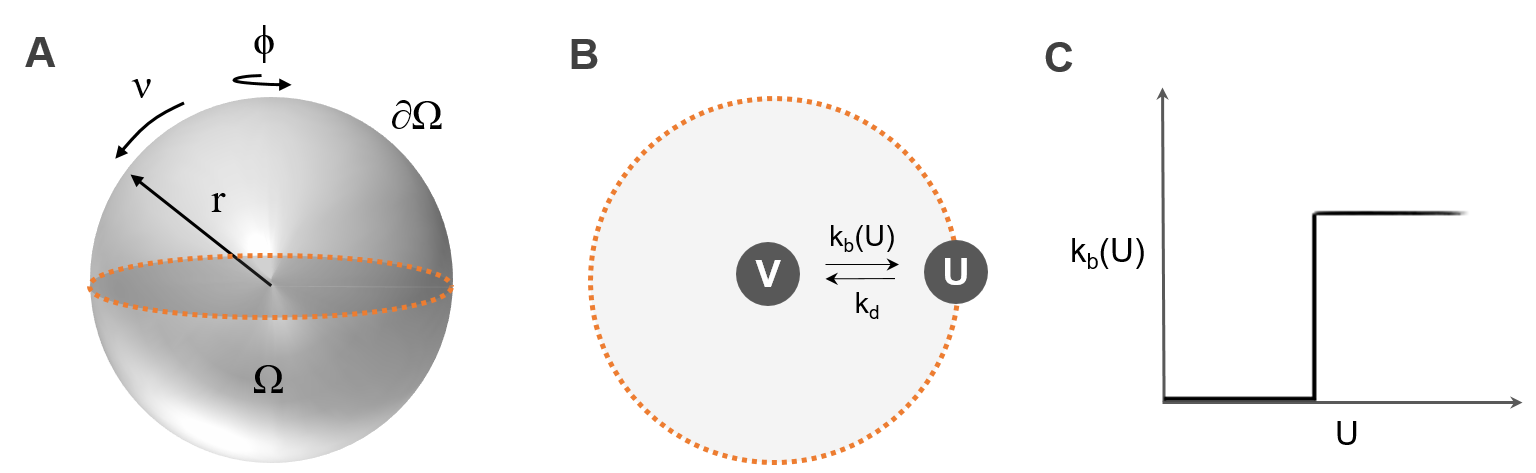
I have just submitted a paper about the modeling of embryogenesis with the Shvartsman group at Princeton University. Let me review the main ideas of our work.

I have just submitted a paper about nonlocal equations on the sphere with my colleagues Mikael Slevinsky and Qiang Du. Here are the main ideas of our work.

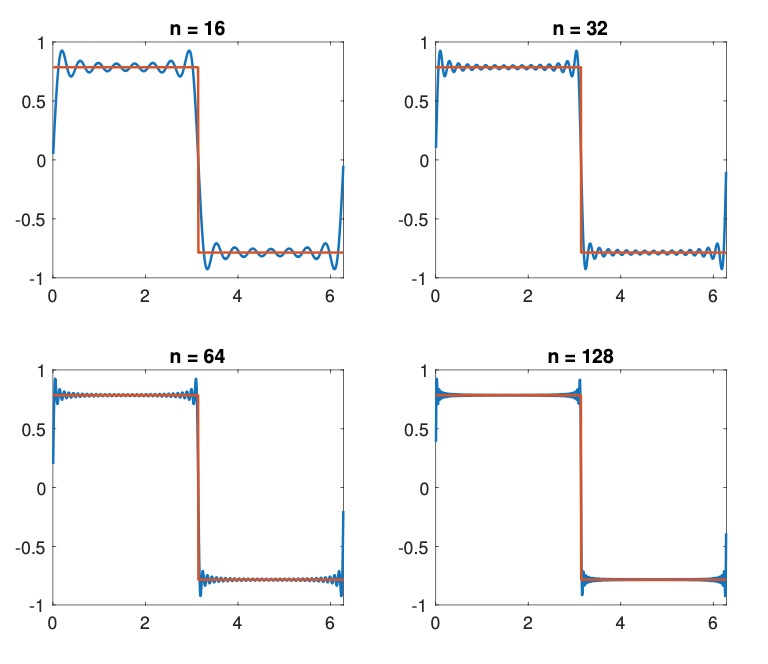
In this post, I talk about a fascinating subject: the convergence of Fourier series and the Gibbs phenomenon.

I started working on deep learning models when I began my research at Columbia University in September 2017. Coming from the approximation theory world, I wanted to learn about their approximation properties. A few months down the road Qiang Du and I have proven a new theorem concerning the approximation of multivariate functions by deep ReLU networks.

My latest paper, with my former colleague Yuji Nakatsukasa, has just been accepted in SISC. In this post, I review the main ideas of our work.

My second paper as a Ph.D. student, in collaboration with my friend and former colleague at Oxford Nikola Gushterov, was about the choreographies of the \(n\)-body problem. These are very simple periodic solutions of the \(n\)-body problem, in which the bodies share a common orbit and are uniformly spread along it; see, e.g., these animations. The trivial ones are circles, and these were found by Lagrange in 1772. Fore more than two centuries, this was the full story.