February 27, 2018 — Support my next blog post, buy me a coffee ☕.
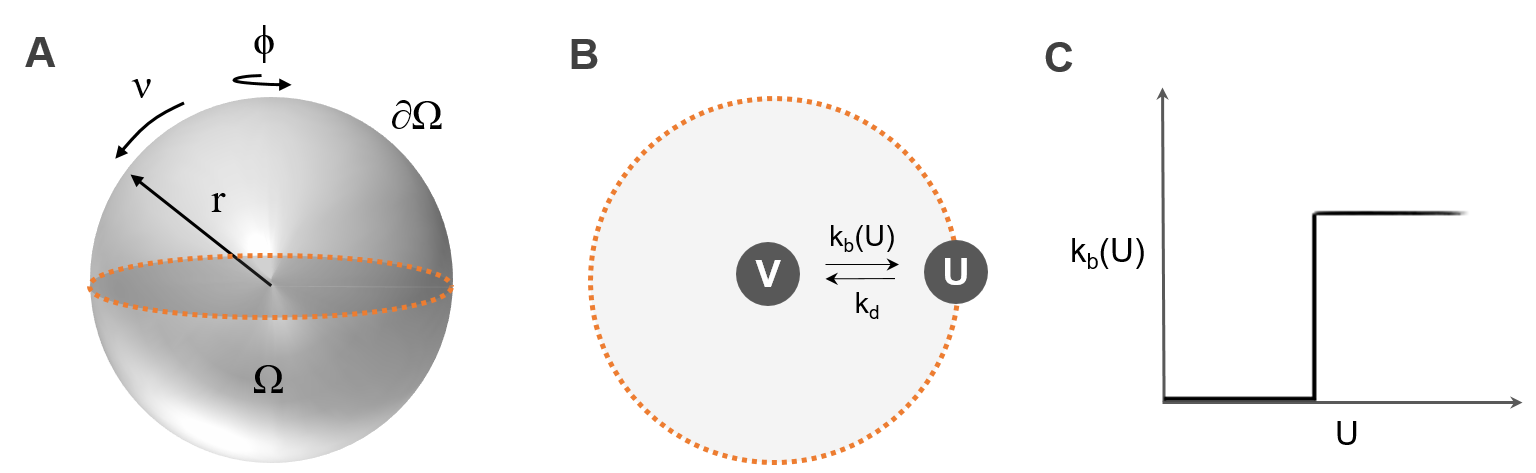
I have just submitted a paper about the modeling of embryogenesis with the Shvartsman group at Princeton University. Let me review the main ideas of our work.
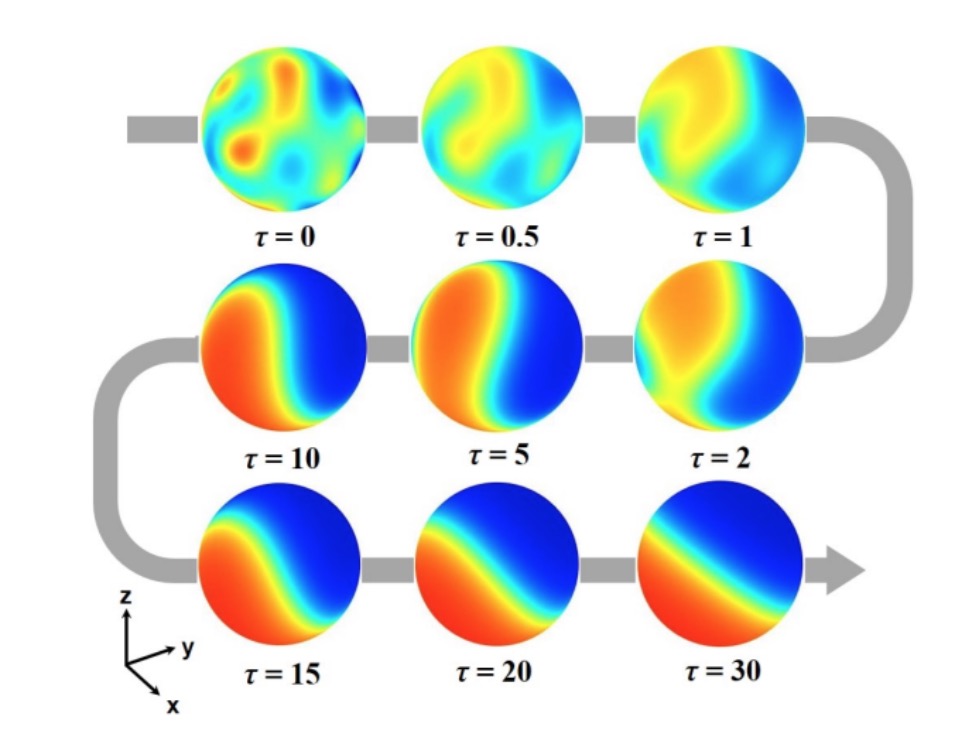
We proposed a new model for the formation of polarized patterns observed in early embryogenesis of C. elegans where mass conservation is the driving force. In our model, a species \(V\) moves freely in a cell \(\Omega\) and reversibly adheres to the cell membrane \(\partial\Omega\). The membrane-bound species \(U\) diffuses on the surface and recruits more of itself to the membrane. For a sphere of radius \(r\), \(U\) and \(V\) satisfy the following equations, $$ \left\{ \begin{array}{l} U_t = \frac{D_U}{r^2}\Delta U + k_b\big(U_0 + H(U - \Gamma)\big)V - k_d U \;\text{on $\partial\Omega$}, \\[1.5pt] V_t = D_V\Delta V\;\text{in $\Omega$}, \\[1.5pt] D_V\nabla V\cdot n = -k_b\big(U_0 + H(U - \Gamma)V\big) + k_d U, \end{array} \right. $$ for some constants \(D_U\), \(D_V\), \(k_b\), \(k_d\), \(\Gamma\) and \(U_0\). Upon nondimensionalization by \(u=k_dU/k_bV_0\), we obtain a single PDE $$ u_\tau = \delta^2\Delta u + \big(1 - \alpha\bar{u}\big)\big(\beta+H(u - \gamma)\big) - u. $$ Using the algorithms presented in a previous blog post, we showed that for arbitrary initial conditions, the only non-uniform long-term behavior was a single axisymmetric spherical cap:
We also showed that, starting from a constant initial condition, transient convection is enough to start the polarization process:
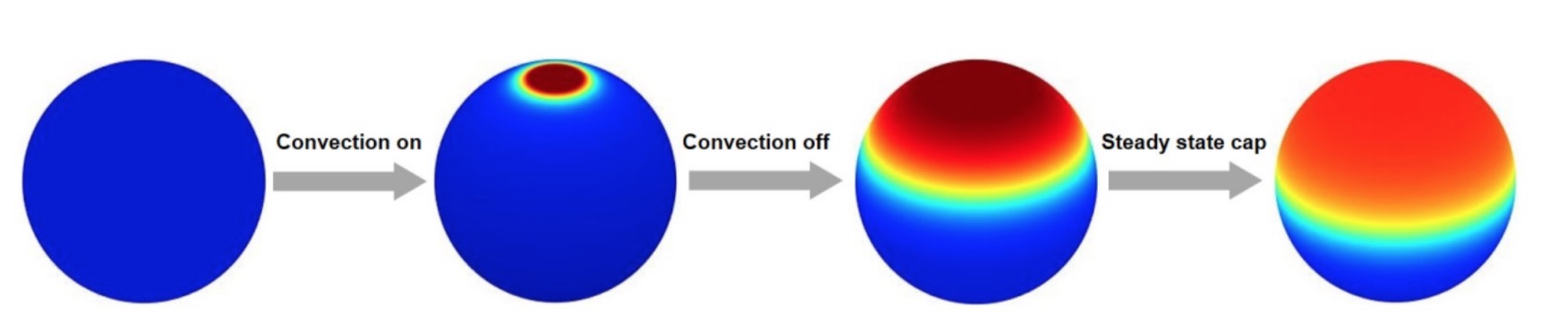
These findings reinforce the idea that symmetry breaking is crucial for the development of all living organisms.
Blog posts about spectral methods
2020 Exponential integrators for stiff PDEs
2018 Computer-assisted proofs for PDEs
2018 Spherical caps in cell polarization
2018 Solving nonlocal equations on the sphere
2018 Gibbs phenomenon and Cesàro mean
2017 Solving PDEs on the sphere
2017 When planets dance