January 4, 2018 — Support my next blog post, buy me a coffee ☕.
In this post, I talk about a fascinating subject: the convergence of Fourier series and the Gibbs phenomenon.
Periodic continuous functions \(f\) of bounded variation have a unique and uniformly convergent Fourier series, that is, the partial sums $$ f_n(\theta) = \sum_{k=0}^{n}a_k\cos(k\theta) + \sum_{k=1}^{n}b_k\sin(k\theta), $$ with Fourier coefficients $$ a_k = \frac{1}{\pi}\int_0^{2\pi}f(\theta)\cos(k\theta)d\theta, $$ and $$ b_k = \frac{1}{\pi}\int_0^{2\pi} f(\theta) \sin(k\theta)d\theta, $$ converge uniformly to \(f\). (Note that \(1/\pi\) is changed to \(1/(2\pi)\) for \(a_0\).) We write $$ f(\theta) = \sum_{k=0}^{\infty}a_k\cos(k\theta) + \sum_{k=1}^{\infty}b_k\sin(k\theta). $$
For functions \(f\) that are merely of bounded variation, the convergence is only pointwise: at every point \(\theta\), the partial sums converge to \(\frac{1}{2}[f(\theta^-) + f(\theta^+)]\); in particular, these converge to \(f(\theta)\) at every point of continuity. What happens at points of discontinuity?
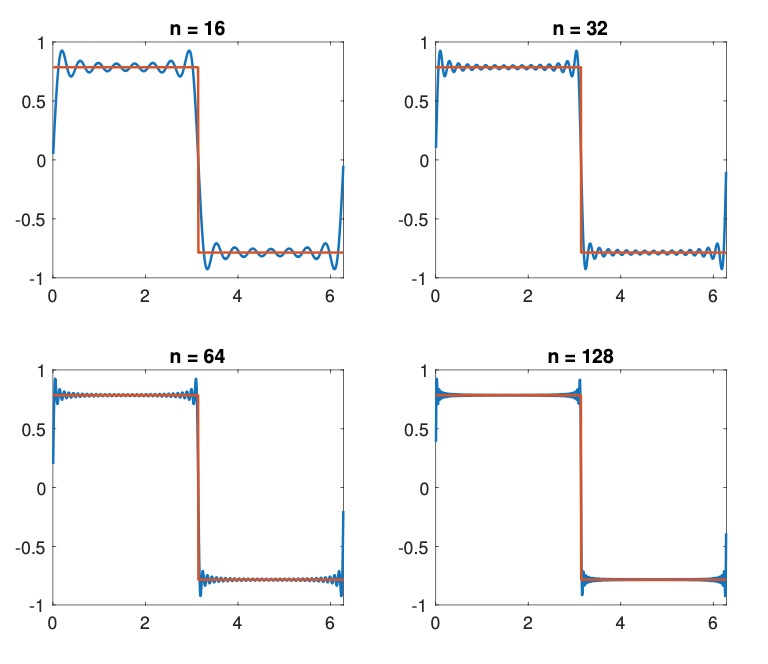
A classical example is the square wave $$ f(\theta) = \frac{\pi}{4}\mathrm{sign}(\pi - \theta), \quad \theta\in[0,2\pi]. $$ This function is of bounded variation and discontinuous at \(0\), \(\pi\) and \(2\pi\). Its Fourier coefficients can be computed analytically and are given by $$ a_k = 0, \quad b_{2k} = 0, \quad b_{2k+1} = \frac{1}{2k+1}. $$ When we compute the partial sums for \(n=16,32,64,128\) we obtain the picture at the top. This is the so-called Gibbs phenomenon, which involves both the fact that the partial sums overshoot at a discontinuity and that this overshoot does not disappear as more terms are added to the sums. The overshoot at \(0\), \(\pi\) and \(2\pi\) is known exactly and is given by $$ \frac{1}{2}\int_0^{\pi}\frac{\sin(\theta)}{\theta}d\theta - \frac{\pi}{4} = \frac{\pi}{2}\times(0.0895\ldots), $$ or about \(9\%\) of the jump. Note that, as \(n\) increases, the position of the overshoot moves closer to the discontinuity. The Gibbs phenomenon is a very standard result that most (applied) mathematicians know.
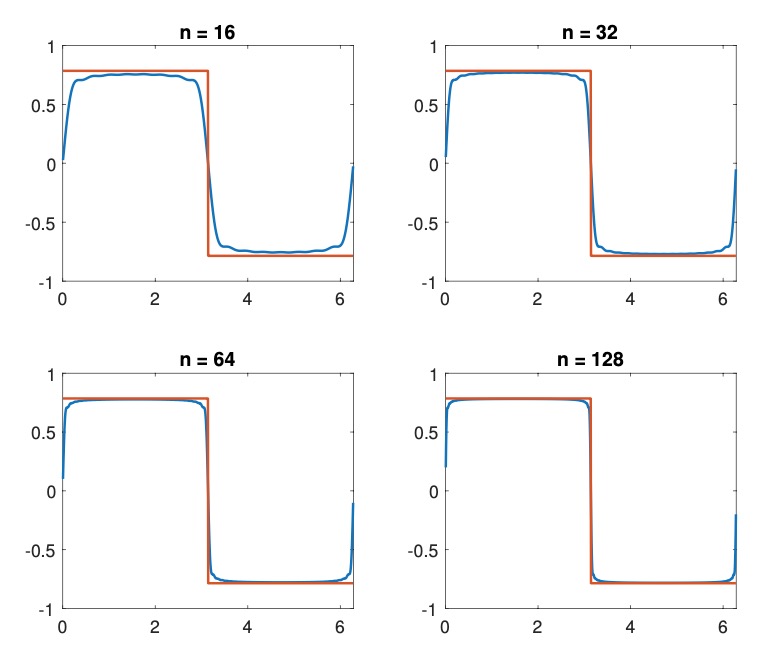
What is perhaps less known is a simple cure using the \((C,1)\) Cesàro mean of the partial sums, which is simply the arithmetic mean, $$ \sigma_n(\theta) = \frac{1}{n+1}\sum_{k=0}^{n}f_k(\theta). $$ For integrable functions \(f\), one can show that \(\sigma_n(\theta)\) converges to \(\frac{1}{2}[f(\theta^-) + f(\theta^+)]\); in particular, this converges to \(f(\theta)\) at every point of continuity, and for continuous functions the convergence is uniform—this is Fejér's thereom. Moreover, if \(m\leq f(\theta)\leq M\) then \(m\leq \sigma_n(\theta)\leq M\). Therefore, the \((C,1)\) Cesàro mean does not show the Gibbs phenomenon, as the following figure illustrates:
With Mikael Slevinsky, we are using the \((C,2)\) Cesàro mean for spherical harmonic expansions on the sphere to post-process numerical solutions of nonlocal PDEs—the paper is coming soon!
Blog posts about spectral methods
2020 Exponential integrators for stiff PDEs
2018 Computer-assisted proofs for PDEs
2018 Spherical caps in cell polarization
2018 Solving nonlocal equations on the sphere
2018 Gibbs phenomenon and Cesàro mean
2017 Solving PDEs on the sphere
2017 When planets dance