Research - H. Montanelli

Research interests

My general research interests lie in numerical methods for PDEs and integral equations, inverse problems, scientific machine learning, and approximation theory. More generally, my background is in numerical analysis and scientific computing. I highlight below my contributions to the following four topics:

Inverse acoustic scattering;
Boundary element methods;
Neural network approximation theory;
Spectral methods.

Inverse acoustic scattering

Background

A typical inverse scattering problem is the identification of the shape of a defect inside a medium by sending waves that propagate within. In the data acquisition step, several sensors record the medium's response that forms the data of the inverse problem; in the data processing step, numerical algorithms are used to recover an approximation of the shape from the measurements. What I have just described is an example of active imaging, where both the sources and the sensors are controlled during the acquisition step. In passive imaging, only sensors are employed and the illumination comes from uncontrolled, random sources. In this setup, it is the cross-correlations between the recorded signals that convey information about the medium through which the waves propagate. While there were many techniques available for inverse scattering problems in active imaging, only linearization approaches had been developed so far in passive imaging.

Results

In 2023, my colleagues and I presented an extension of the linear sampling method for solving the sound-soft inverse acoustic scattering problem with randomly distributed point sources. The theoretical justification of my sampling method is based on the Helmholtz–Kirchhoff identity, the cross-correlation between measurements, and the volume and imaginary near-field operators, which we introduced and analyzed. The resulting method gives comparable results to the standard linear sampling method with deterministic sources. In 2024, we extended it to the case of data generated by small random scatterers—a seemingly simple yet powerful model of a random medium that allowed us to apply the linear sampling method in a novel manner.

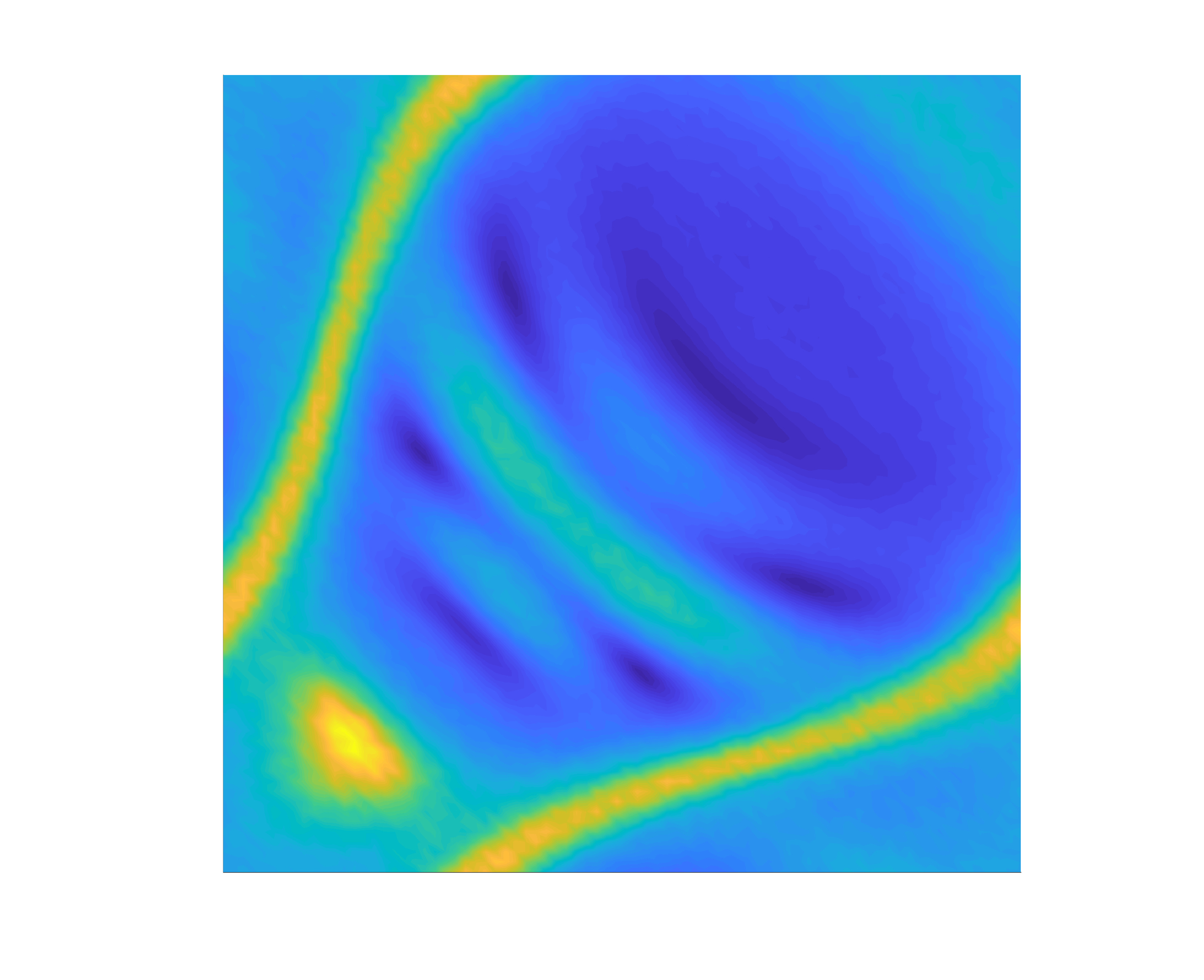
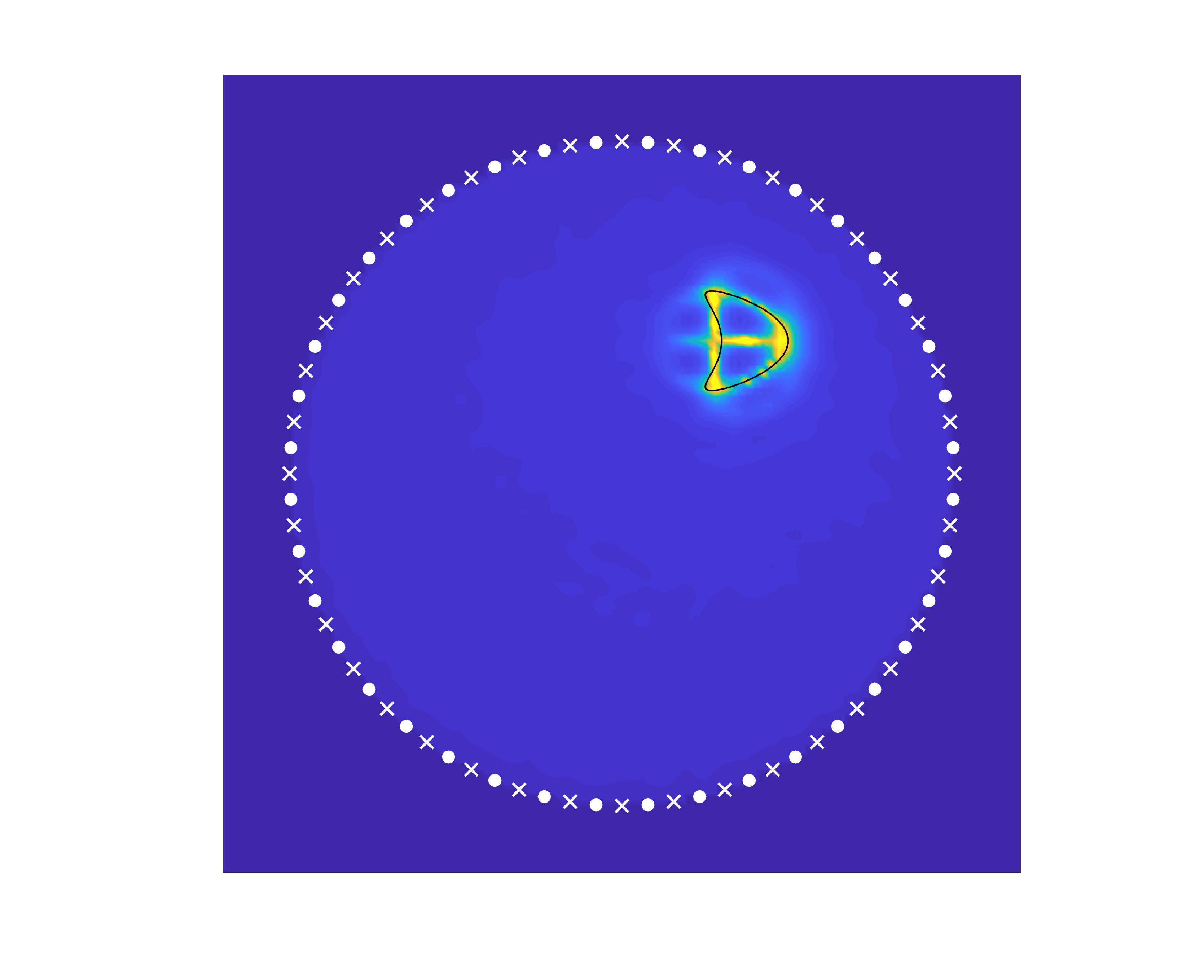
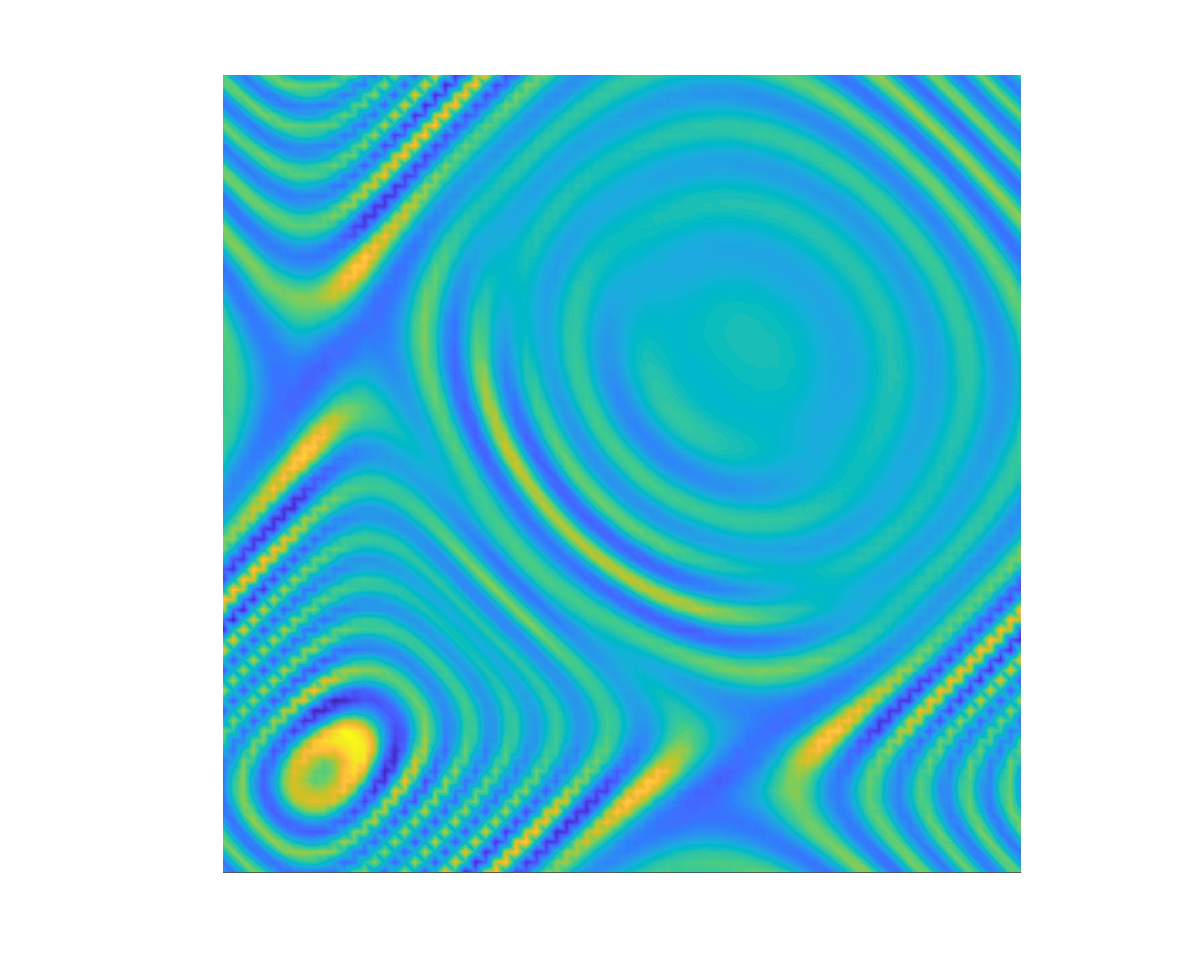
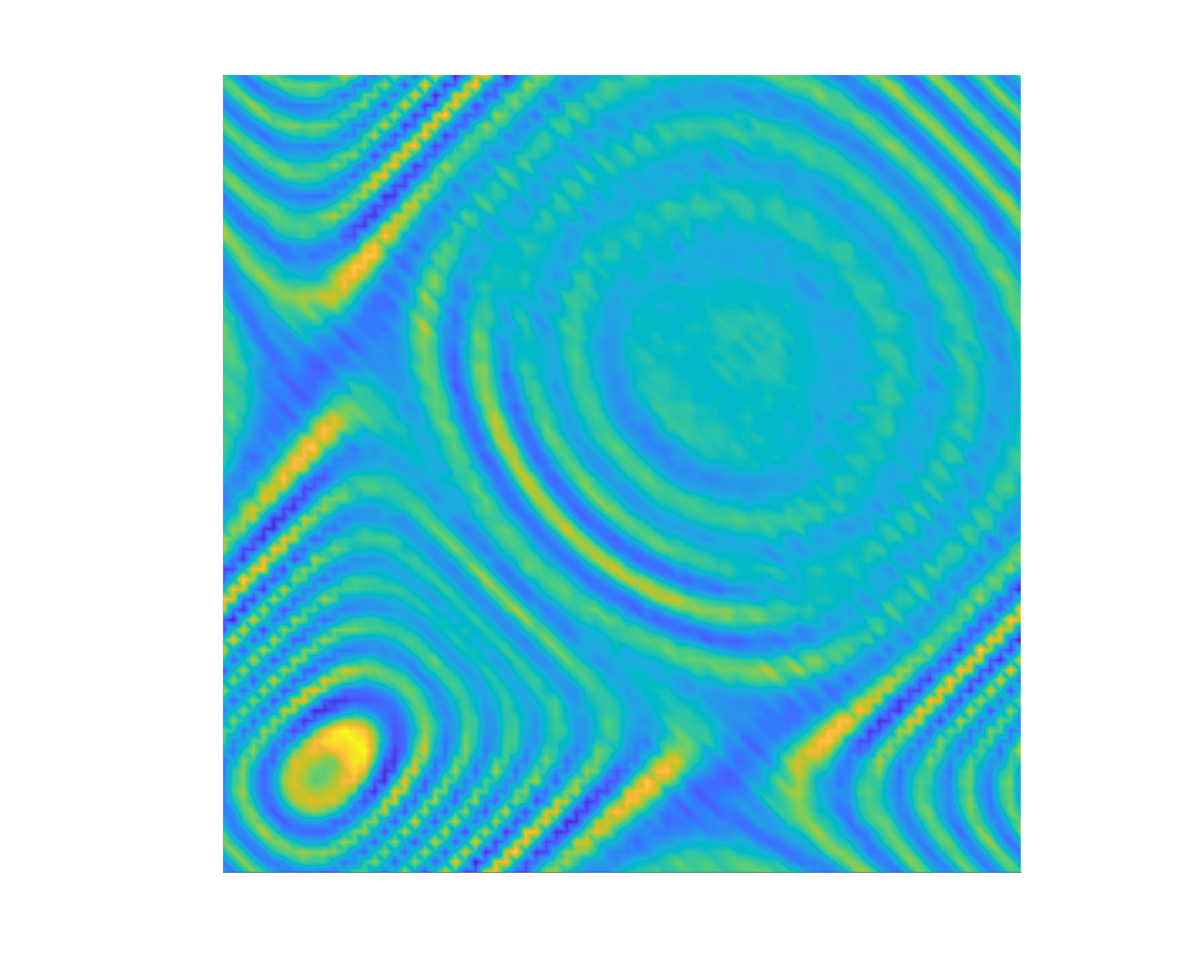
Collaborators

Josselin Garnier (École Polytechnique), Houssem Haddar (Inria)

Software

lsmlab — MATLAB package for solving inverse acoustic problems with the LSM

Papers

2024 The linear sampling method for data generated by small random scatterers doi arXiv

2023 The linear sampling method for random sources doi arXiv

Blog posts

2024 The linear sampling method for small random scatterers

2022 The linear sampling method for random sources

Boundary element methods

Background

The Helmholtz equation $\Delta u + k^2u = 0$ in the presence of an obstacle may be rewritten as an integral equation on the obstacle's boundary via layer potentials. For example, the radiating solution to the exterior Dirichlet problem $\Delta u + k^2u = 0$ in $\mathbb{R}^3\setminus\overline{D}$ with $u = u_D$ on $\partial D$, for some bounded $D$ whose complement is connected, can be obtained via the equation $$ \int_{\partial D}G(\boldsymbol{x},\boldsymbol{y})\varphi(\boldsymbol{y})dS(\boldsymbol{y}) = u_D(\boldsymbol{x}), \quad \boldsymbol{x}\in\partial D, $$ based on the single-layer potential; $G$ is the Green's function of the Helmholtz equation in 3D. Once the integral equation is solved for $\varphi$, the solution $u$ may be represented by the left-hand side for all $\boldsymbol{x}\in\mathbb{R}^3\setminus\overline{D}$. From a numerical point of view, such integral equations are particularly challenging for several reasons. First, when $\boldsymbol{x}$ approaches $\boldsymbol{y}$, the integral becomes singular and standard quadrature schemes fail to be accurate—analytic integration or carefully-derived quadrature formulas are required. Second, the resulting linear systems after discretization are dense. For large wavenumbers $k$, only iterative methods can be used to solve them (with the help of specialized techniques to accelerate the matrix-vector products such as hierarchical matrices). In this respect, the use of high-order schemes may be helpful in enlarging the interval of feasible wavenumbers.

Results

In 2022, my colleagues and I presented algorithms for computing weakly singular and near-singular integrals arising with high-order boundary elements. We utilized the continuation approach in a novel way that simplifies implementation, decreases computational costs, and carefully handles both singular and near-singular integrals—existing methods are designed for singular integrals but are not accurate in the near-singular case. More generally, the paper utilizes a variety of numerical tools (e.g., Newton's method, transplanted Gauss quadrature). The resulting method is applicable to any 3D object, including resonant cavities and thin layers. These algorithms were extended to the strongly singular case in 2024. Implementations in C++ and Python can be found in the fembem and singintpy packages.

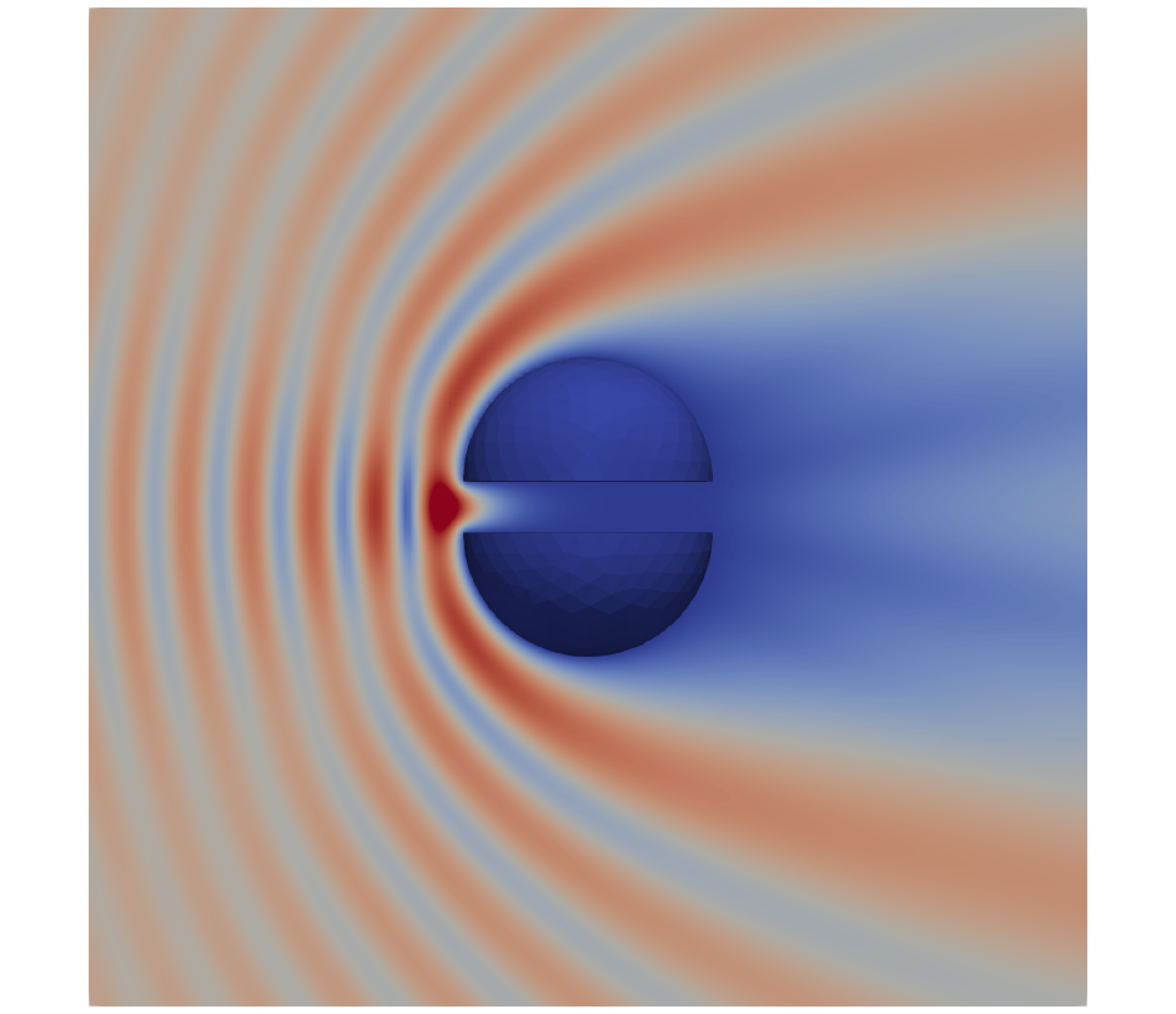
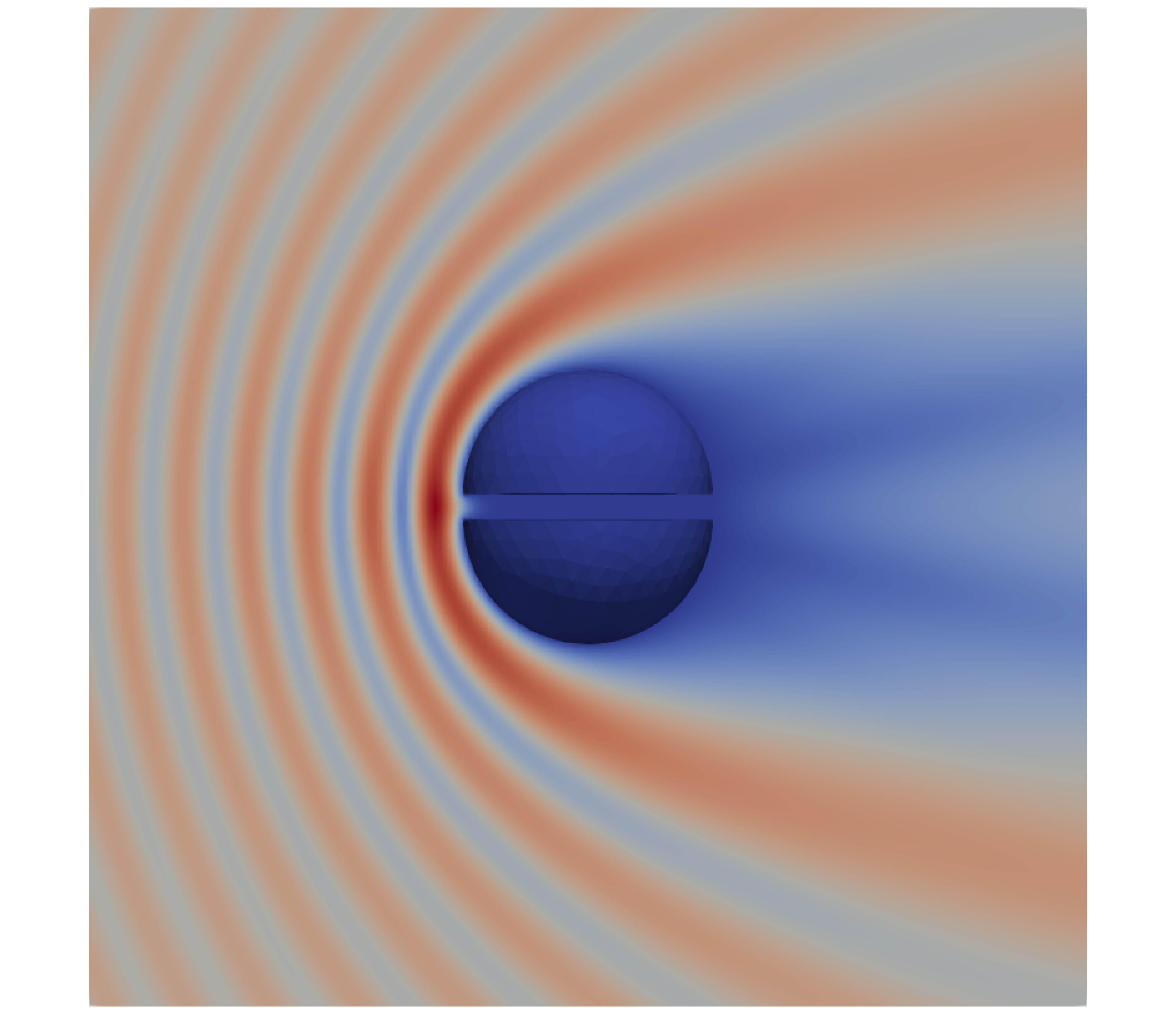
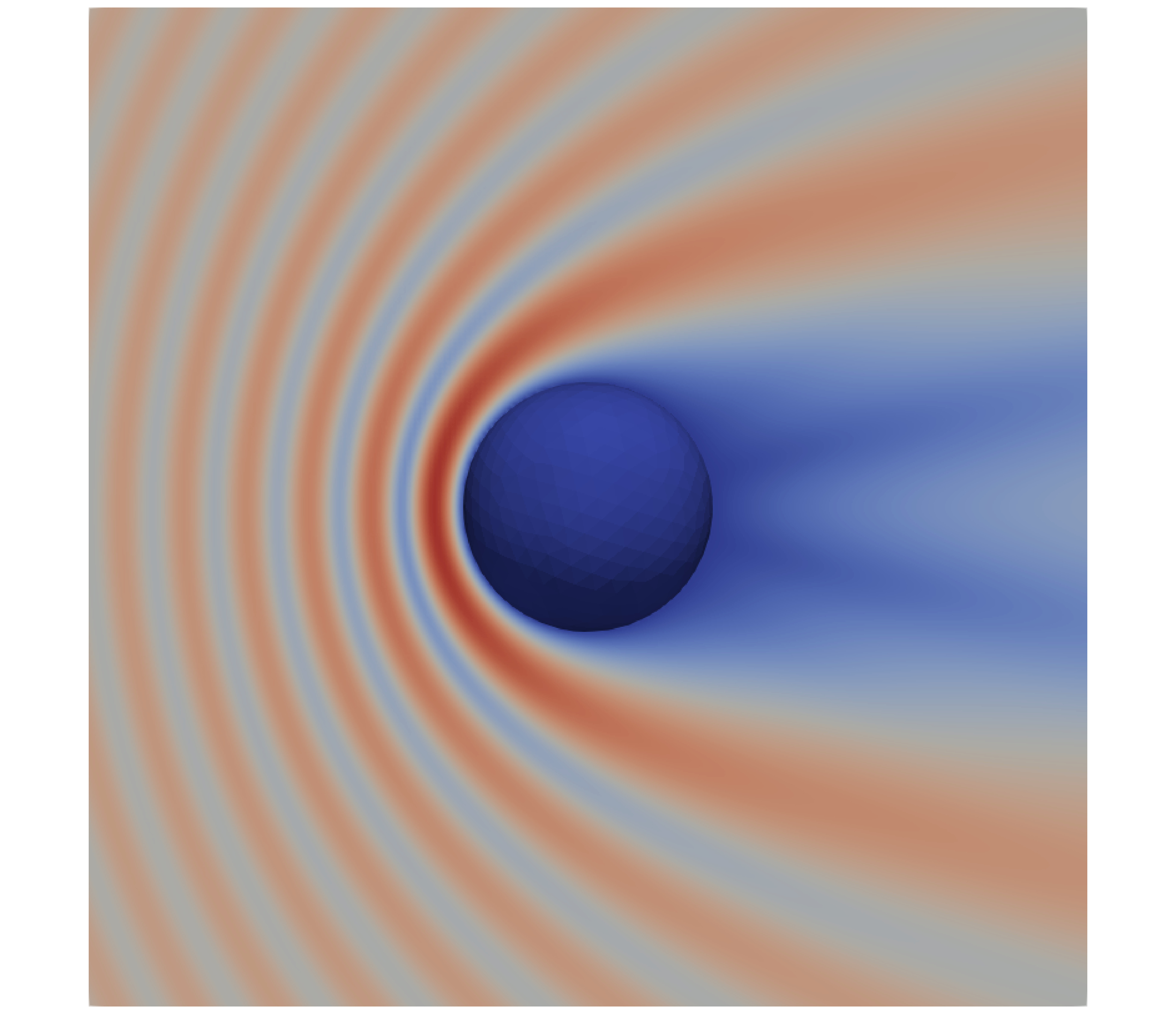
Collaborators

Matthieu Aussal (École Polytechnique), Francis Collino & Houssem Haddar (Inria)

Software

fembem — C++ package to solve scattering problems with BEMs

singintpy — Python package for computing singular & near-singular integrals on quadratic triangles

Papers

2023 Computing singular and near-singular integrals over curved boundary elements: Strongly singular case doi arXiv

2022 Computing weakly singular and near-singular integrals over curved boundary elements doi arXiv

Blog posts

2023 Strongly singular integrals over curved elements

2023 Finite-boundary element coupling in MATLAB

2021 Weakly singular integrals over curved elements

Neural network approximation theory

Background

I am interested in the mathematical properties of neural network models. In particular, I am trying to understand why and when neural networks break the curse of dimensionality.

For a real-valued function $f$ in $\mathbb{R}^d$ whose smoothness is characterized by some integer $m$ (typically the order of integrable or bounded derivatives) and for some prescribed $\epsilon>0$, one tries to show that there exists a neural network $f_W$ of size $W$ that satisfies, for some norm $\Vert\cdot\Vert$, $$ \Vert f - f_W \Vert \leq \epsilon \quad \text{with} \quad W=\mathcal{O}(\epsilon^{-\frac{d}{m}}). $$ For deep neural networks, one also wants to find the asymptotic behavior of the depth $L$ as a function of the error $\epsilon$. (Note that the size $W$ is the total number of parameters while the depth $L$ is the number of hidden layers.) Results of this form are standard approximation results that suffer from the curse of dimensionality: for small dimensions $d$, the size $W$ of the network increases at a reasonable rate as $\epsilon$ goes to zero; however, $W$ grows geometrically with $d$.

Results

In 2019, my collaborators and I showed that functions in the so-called Korobov spaces $X^{2,p}(\Omega)$ of mixed derivatives in $\Omega\subset\mathbb{R}^d$ can be approximated with error $\epsilon$ by neural networks of depth $L=\mathcal{O}(\vert\log\epsilon\vert\log d)$ and size $W=\mathcal{O}(\epsilon^{-\frac{1}{2}}\vert\log\epsilon\vert^{\frac{3}{2}(d-1)+1}(d-1))$. The curse of dimensionality is lessened since $d$ only affects logarithmic factors.

In 2020, we used the Kolmogorov–Arnold theorem to show that a subset of the continuous functions in $[0,1]^d$ can be approximated with error $\epsilon$ by neural networks of depth and size $L,W=\mathcal{O}(\epsilon^{-\log d})$.

Finally, in 2021, we considered generalized bandlimited functions $f:[0,1]^d\rightarrow\mathbb{R}$ of the form $$ f(\boldsymbol{x}) = \int_{\mathbb{R}^d}F(\boldsymbol{w})K(\boldsymbol{w}\cdot\boldsymbol{x})d\boldsymbol{w}, $$ with $\mathrm{supp}\,F\subset [-M,M]^d$, $M\geq 1$, and for some integrable function $F:[-M,M]^d\rightarrow\mathbb{C}$ and analytic kernel $K:\mathbb{R}\rightarrow\mathbb{C}$. We proved that such functions can be approximated with error $\epsilon$ by neural networks of depth $L=\mathcal{O}(\log^2\epsilon^{-1})$ and size $W=\mathcal{O}(\epsilon^{-2}\log^2\epsilon^{-1})$.

Collaborators

Qiang Du (Columbia), Haizhao Yang (Maryland)

Software

learnpy — Python package for supervised & unsupervised learning

Papers

2021 Deep ReLU networks overcome the curse of dimensionality for generalized bandlimited functions doi arXiv

2020 Error bounds for deep ReLU networks using the Kolmogorov–Arnold superposition theorem doi arXiv

2019 New error bounds for deep ReLU networks using sparse grids doi arXiv

Blog posts

2019 Deep networks and the Kolmogorov–Arnold theorem

2019 Deep networks and bandlimited functions

2017 Deep networks and the curse of dimensionality

Spectral methods

Background

Orthogonal polynomials lie at the heart of scientific computing. In the last ten years, there has been a renewed interest in their properties, which has contributed to the development of more efficient algorithms. In particular, asymptotic expansions and the exploitation of sparsity and low-rank structure in recurrence relations have been some of the key ingredients in the design of packages such as chebfun (MATLAB), approxfun (Julia), and dedalus (Python), which have automated the computation with orthogonal polynomials for approximating functions via interpolation, computing integrals via quadrature, and solving differential equations via spectral methods.

These packages are particularly relevant to the astrophysics, computational fluid dynamics, and biology communities, where simple geometries such as the sphere are prevalent. For example, nonlinear advection equations on the sphere, such as the shallow water equations, are of significant importance in atmospheric numerical modeling, while reaction-diffusion equations in a spherical shell are widely used as a model for convection patterns within the Earth's mantle, as well as for the modeling of morphogenesis in embryos. On top of these standard local differential equations, their nonlocal integral analogs are becoming more and more popular to model a wide range of phenomena in these communities.

Results

My Ph.D. introduced new numerical methods for the simulation of periodic physical phenomena.

The first year of my Ph.D. work was about the computation with periodic functions via approximations by trigonometric polynomials to machine precision, including the solution of nonlinear ODEs and ODE eigenvalue problems. For example, the Sturm–Liouville problem with periodic boundary conditions, $$ -\frac{d}{d\theta}\Big[p(\theta)\frac{du}{d\theta}\Big]+q(\theta)u(\theta)=\lambda w(\theta)u(\theta), $$ is discretized by $(-\mathbf{D}_N\mathbf{M}[p]\mathbf{D}_N + \mathbf{M}[q])\widehat{u} = \lambda\mathbf{M}[w]\widehat{u}$, where $\mathbf{D}_N$ and $\mathbf{M}[f]$ are the differentiation and multiplication by $f$ matrices in Fourier space, and $\widehat{u}$ is the vector of Fourier coefficients of $u$.

During my second year, I investigated the computation of choreographies, periodic solutions in time of the $n$-body problem in which the bodies share a common orbit. The $n$-body problem describes the motion of $n$ point particles $z_j(t)\in\mathbb{C}$, $0\leq j\leq n-1$, through $$ z_j^{''}(t) - \sum_{\underset{i\neq j}{i=0}}^{n-1} \frac{z_i(t) - z_j(t)}{\big\vert z_i(t) - z_j(t) \big\vert^3} = 0, \;\, 0\leq j\leq n-1. $$ Since choreographies share a single orbit and are uniformly spread along it, these can be written as $z_j(t) = q(t + 2\pi j/n)$, for some $2\pi$-periodic function $q:[0,2\pi]\rightarrow\mathbb{C}$, and are minima of the action $$ \begin{align} A = \frac{n}{2}\int_0^{2\pi} \big\vert q'(t) \big\vert^2 dt + \frac{n}{2}\sum_{j=1}^{n-1} \int_0^{2\pi} \Big\vert q(t) - q\Big(t + \frac{2\pi j}{n}\Big) \Big\vert^{-1}dt. \end{align} $$ My coauthor and I proposed an algorithm based on interpolation and optimization for computing choreographies, which we implemented in the choreolab MATLAB package.

In my third year, I worked on stiff PDEs of the form $$ u_t = \mathcal{L}u + \mathcal{N}(u), \quad u(0,\boldsymbol{x})=u_0(\boldsymbol{x}), $$ where $u(t,\boldsymbol{x})$ is a function of time $t$ and space $\boldsymbol{x}$, $\mathcal{L}$ is a linear differential operator on a spatial domain in one, two or three periodic space dimensions and $\mathcal{N}$ is a nonlinear operator of lower order. My colleague and I compared 30 high-order exponential integrators and showed that is it hard to beat one of the simplest integrators. Implementations in the chebfun MATLAB package allow one to compute the solutions of many PDEs quickly and accurately (spin code). We also implemented some of these integrators in the chebpy Python package.

The main project of my final year at Oxford was on stiff PDEs on the unit sphere of the form $$ u_t = \mathcal{L}u + \mathcal{N}(u), \;\; u(t=0,x,y,z)=u_0(x,y,z). $$ My coauthor and I proposed a novel fast algorithm based on a variant of the double Fourier sphere method and implicit-explicit time-stepping schemes (spinsphere code).

With discretizations of operators in hand, I explored potential applications in biology during a postdoc at Columbia. I used the fast algorithms we developed to investigate pattern formation and explain symmetry breaking on the sphere with colleagues at Princeton.

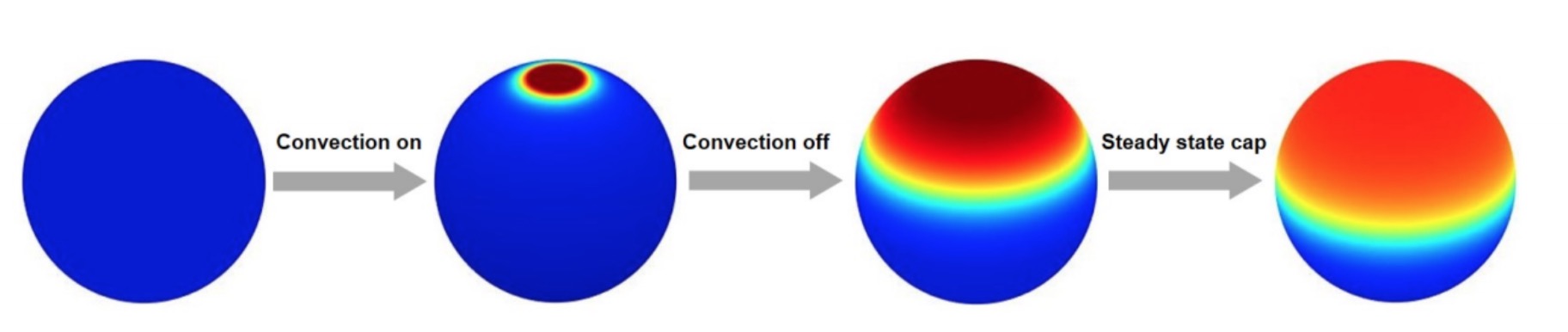
My collaborators and I also introduced nonlocal diffusion operators on the sphere $\mathbb{S}^2$, $$ \mathcal{L}_\delta u(\boldsymbol{x}) = \int_{\mathbb{S}^2} \rho_\delta(\vert\boldsymbol{x}-\boldsymbol{y}\vert) [u(\boldsymbol{y}) - u(\boldsymbol{x})]\,d\Omega(\boldsymbol{y}), $$ where$\rho_\delta$ is a suitably defined (singular) nonlocal kernel. We presented algorithms for solving PDEs involving such operators with spectral accuracy in space and high-order accuracy in time. These are based on the diagonalization of the nonlocal operators, the high-accuracy computation of their eigenvalues, a fast spherical harmonic transform, and exponential integrators.