October 2, 2023
In this post, I talk about a new method for computing strongly singular and near-singular integrals that arise when solving the 3D Helmholtz equation with curved boundary elements.
Background on integral equations
The Helmholtz equation, which has the form $$ \Delta u + k^2u = 0, $$ appears when one looks for time-harmonic solutions to the wave equation—if \(v(\boldsymbol{x},t)=u(\boldsymbol{x})e^{-i\omega t}\) is a solution to \(v_{tt}=c^2\Delta v\), then \(u\) satisfies the Helmholtz equation with wavenumber \(k=\omega /c\). It is of fundamental importance in science and engineering, with applications as diverse as noise scattering, radar and sonar technology, and seismology. For instance, given an incident acoustic wave \(u^i\) that is a solution to the Helmholtz equation in \(\mathbb{R}^3\), the outgoing scattered field \(u^s\) generated by a bounded obstacle \(D\) is also a solution to Helmholtz equation, in \(\mathbb{R}^3\setminus\overline{D}\), with \(u^i+u^s=0\) on the boundary \(\partial D\) (for sound-soft scattering).
For obstacles \(D\) whose complements are connected, a popular technique for calculating scattered fields is based on integral equations. As an example, one can show that the solution \(u^s\) to the sound-soft scattering problem of the previous paragraph may be obtained by solving $$ \int_{\partial D}\left\{\frac{\partial G(\boldsymbol{x},\boldsymbol{y})}{\partial\boldsymbol{n}(\boldsymbol{y})} - i\eta G(\boldsymbol{x},\boldsymbol{y})\right\}\varphi^s(\boldsymbol{y})dS(\boldsymbol{y}) + \frac{\varphi^s(\boldsymbol{x})}{2} = -u^i(\boldsymbol{x}), \;\; \boldsymbol{x}\in\partial D, $$ for some arbitrary real number \(\eta\neq0\) such that \(\eta\mathrm{Re}(k)\geq0\). Once the equation is solved for \(\varphi^s\), the scattered field is given by $$ u^s(\boldsymbol{x}) =\int_{\partial D}\left\{\frac{\partial G(\boldsymbol{x},\boldsymbol{y})}{\partial\boldsymbol{n}(\boldsymbol{y})} - i\eta G(\boldsymbol{x},\boldsymbol{y})\right\}\varphi^s(\boldsymbol{y})dS(\boldsymbol{y}), \;\; \boldsymbol{x}\in\mathbb{R}^3\setminus{\overline{D}}. $$ The function \(G\) is the Green's function of the Helmholtz equation in 3D, $$ G(\boldsymbol{x},\boldsymbol{y}) = \frac{1}{4\pi}\frac{e^{ik\vert\boldsymbol{x}-\boldsymbol{y}\vert}}{\vert\boldsymbol{x}-\boldsymbol{y}\vert}. $$
Challenges
One of the challenges one faces when solving integral equations is the computation of singular integrals—when \(\boldsymbol{x}\) is equal to \(\boldsymbol{y}\), the Green's function and its derivatives are unbounded. There are many specialized methods to compute such integrals, including singularity subtraction, singularity cancellation, and the continuation approach. We described, in a previous blog post, algorithms to compute weakly singular integrals using singularity subtraction and the continuation approach. The term weakly singular refers to integrals with singularities of the same type as the Green's function. We describe, here, our method to strongly singular integrals, which have singularities of the same nature as the derivatives of the Green's function.
Computing strongly singular integrals
We consider strongly singular and near-singular integrals of the form $$ I(\boldsymbol{x}_0) = \int_{\mathcal{T}}\frac{(\boldsymbol{x} - \boldsymbol{x}_0)\cdot\boldsymbol{n}(\boldsymbol{x})}{\vert\boldsymbol{x}-\boldsymbol{x}_0\vert^3}\varphi(F^{-1}(\boldsymbol{x}))dS(\boldsymbol{x}), $$ where \(\mathcal{T}\subset\mathbb{R}^3\) is a curved triangle defined by a polynomial transformation \(F:\widehat{T}\to\mathcal{T}\) of degree \(q\geq1\) from some reference planar triangle \(\widehat{T}\subset\mathbb{R}^2\), \(\boldsymbol{x}_0\in\mathbb{R}^3\) is a point on/or close to \(\mathcal{T}\), \(\varphi:\widehat{T}\to\mathbb{R}\) is a polynomial function of degree \(p\geq0\) (not necessarily equal to \(q\), and \(\boldsymbol{n}(\boldsymbol{x})\) is the unit normal vector at \(\boldsymbol{x}\). Our method is based on the computation of the preimage of the singularity in the reference element's space using Newton's method, singularity subtraction with Taylor-like asymptotic expansions, the continuation approach, and transplanted Gauss quadrature.
Step 1. We map \(\mathcal{T}\) back to \(\widehat{T}\), $$ I(\boldsymbol{x}_0) = \int_{\widehat{T}}\frac{(F(\boldsymbol{\widehat{x}})-\boldsymbol{x}_0)\cdot\boldsymbol{\widehat{n}}(\boldsymbol{\widehat{x}})}{\vert F(\boldsymbol{\widehat{x}})-\boldsymbol{x}_0\vert^3}\varphi(\boldsymbol{\widehat{x}})dS(\boldsymbol{\widehat{x}}), $$ where \(\boldsymbol{\widehat{n}}(\boldsymbol{\widehat{x}}) = F_{\widehat{x}_1}(\boldsymbol{\widehat{x}})\times F_{\widehat{x}_2}(\boldsymbol{\widehat{x}})\).
Step 2. We compute \(\boldsymbol{\widehat{x}}_0\in\mathbb{R}^2\) such that \(F(\boldsymbol{\widehat{x}}_0)\in\mathcal{T}\) is the closest point to \(\boldsymbol{x}_0\) on \(\mathcal{T}\) (this is done with numerical optimization). We then decompose \(\boldsymbol{x}_0\) as $$ \boldsymbol{x}_0 = F(\boldsymbol{\widehat{x}}_0) + h\frac{\boldsymbol{\widehat{n}}_0}{\vert\boldsymbol{\widehat{n}}_0\vert}, \quad \boldsymbol{\widehat{n}}_0 = \boldsymbol{\widehat{n}}(\boldsymbol{\widehat{x}}_0), $$ for some scalar \(h\), which may be negative, obtained via $$ h = (\boldsymbol{x}_0 - F(\boldsymbol{\widehat{x}}_0)) \cdot \frac{\boldsymbol{\widehat{n}}_0}{\vert\boldsymbol{\widehat{n}}_0\vert}. $$
Step 3. We compute the strongly singular term, $$ T_{-2}(\boldsymbol{\widehat{x}},h) = -\frac{h\varphi_0\vert\boldsymbol{\widehat{n}}_0\vert}{\left[\vert J_0(\boldsymbol{\widehat{x}} - \boldsymbol{\widehat{x}}_0)\vert^2 + h^2\right]^{\frac{3}{2}}}, $$ where \(J_0\) is the Jacobian matrix at \(\boldsymbol{\widehat{x}}_0\) and \(\varphi_0=\varphi(\boldsymbol{\widehat{x}}_0)\), as well as the weakly singular term \(T_{-1}\). We subtract them from/add them to the integrand, $$ I(\boldsymbol{x}_0) = \, \int_{\widehat{T}}\left[\frac{(F(\boldsymbol{\widehat{x}})-\boldsymbol{x}_0)\cdot\boldsymbol{\widehat{n}}(\boldsymbol{\widehat{x}})}{\vert F(\boldsymbol{\widehat{x}})-\boldsymbol{x}_0\vert^3}\varphi(\boldsymbol{\widehat{x}}) - T_{-2}(\boldsymbol{\widehat{x}},h) - T_{-1}(\boldsymbol{\widehat{x}},h)\right]dS(\boldsymbol{\widehat{x}}) \\ + \int_{\widehat{T}}T_{-2}(\boldsymbol{\widehat{x}},h)dS(\boldsymbol{\widehat{x}}) + \int_{\widehat{T}}T_{-1}(\boldsymbol{\widehat{x}},h)dS(\boldsymbol{\widehat{x}}). $$ The first integral is regularized—it may be computed with Gauss quadrature on triangles. The last two integrals are singular or near-singular and will be computed in steps 4–5.
Step 4. Let $$ \begin{align} I_{-2}(h) = \int_{\widehat{T}}T_{-2}(\boldsymbol{\widehat{x}},h)dS(\boldsymbol{\widehat{x}}), \quad I_{-1}(h) = \int_{\widehat{T}}T_{-1}(\boldsymbol{\widehat{x}},h)dS(\boldsymbol{\widehat{x}}). \end{align} $$ Since \(T_{-2}\) and \(T_{-1}\) are homogeneous in \(\boldsymbol{\widehat{x}}\) and \(h\), using the continuation approach, we reduce the 2D integrals to a sum of three 1D integrals along the edges of the shifted triangle \(\widehat{T}-\boldsymbol{\widehat{x}}_0\). For instance, for \(I_{-2}\), this yields $$ I_{-2}(h) = -\mathrm{sign}(h)\varphi_0\vert\boldsymbol{\widehat{n}}_0\vert\sum_{j=1}^3\widehat{s}_j\int_{\partial\widehat{T}_j-\boldsymbol{\widehat{x}}_0}\frac{\sqrt{\vert J_0\boldsymbol{\widehat{x}}\vert^2 + h^2}-\vert h\vert}{\vert J_0\boldsymbol{\widehat{x}}\vert^2\sqrt{\vert J_0\boldsymbol{\widehat{x}}\vert^2 + h^2}}ds(\boldsymbol{\widehat{x}}), $$ where the \(\widehat{s}_j\)'s are the distances from the origin to the edges of \(\widehat{T}-\boldsymbol{\widehat{x}}_0\).
Step 5. To circumvent near-singularity issues in the computation of \(I_{-2}\) and \(I_{-1}\), we employ transplanted quadrature when the singularity is close to the edges. We take advantage of the a priori knowledge of the singularities to utilize transplanted rules with significantly improved convergence rates.
Numerical experiments
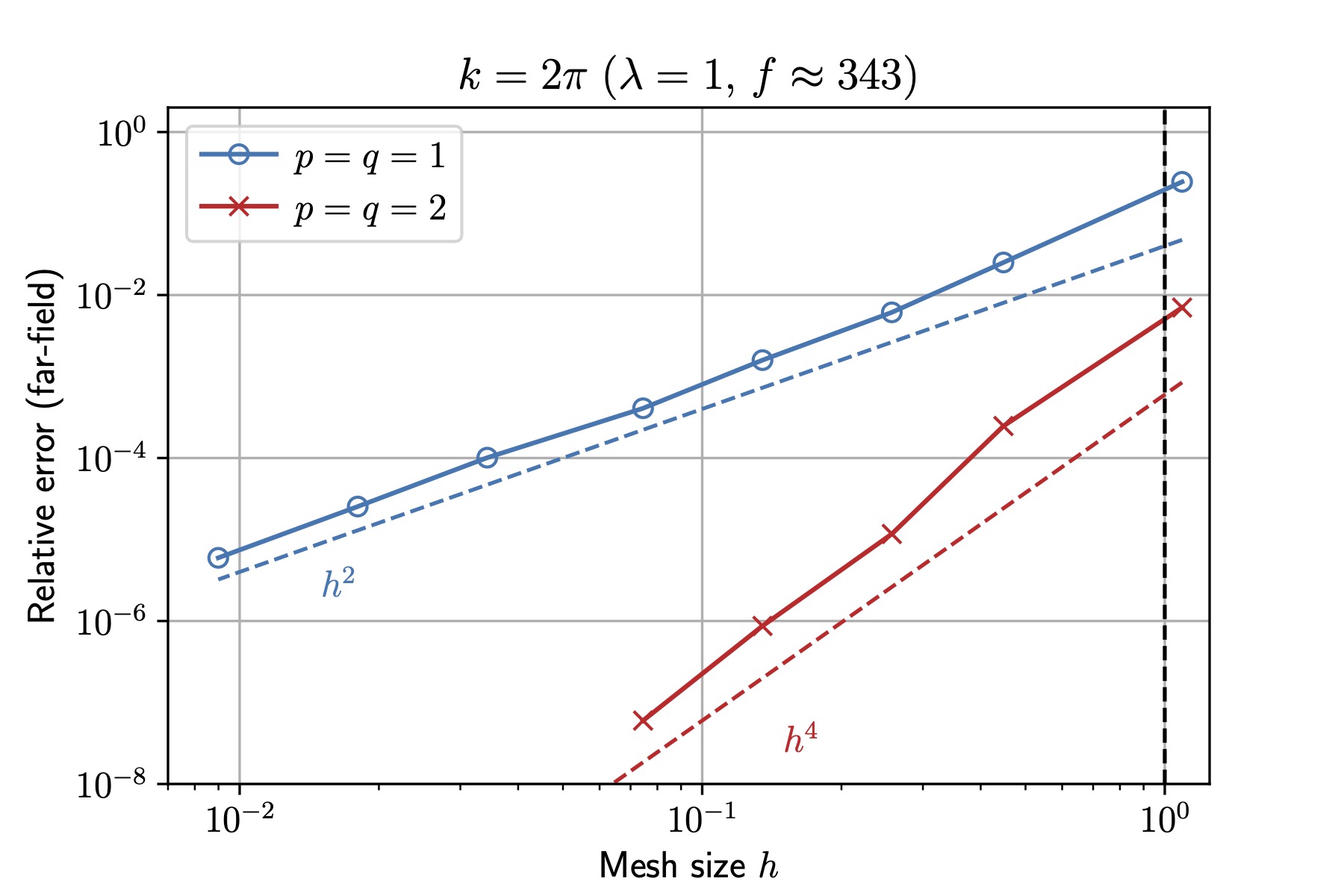
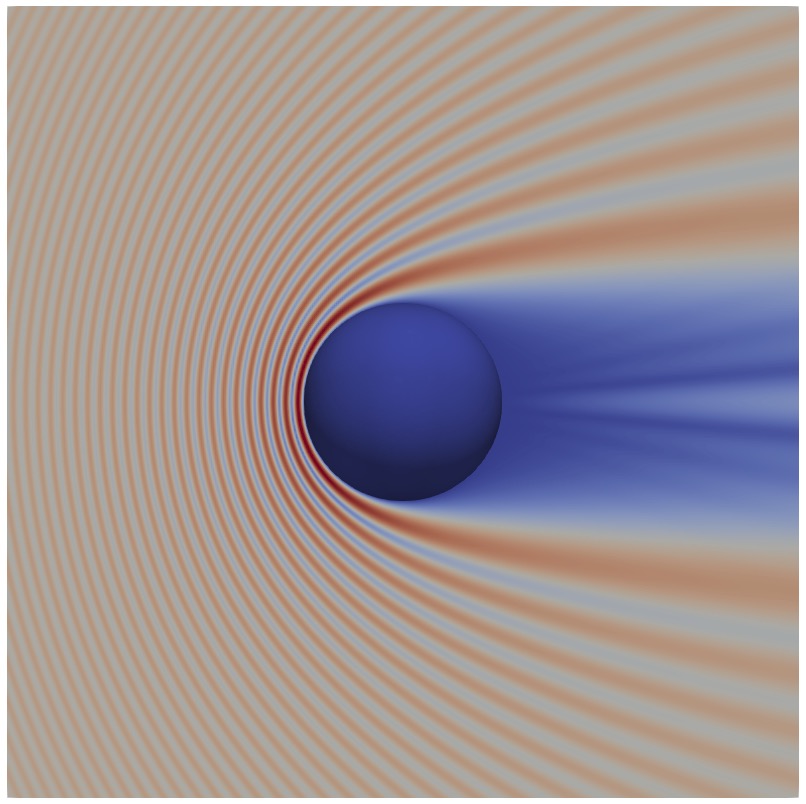
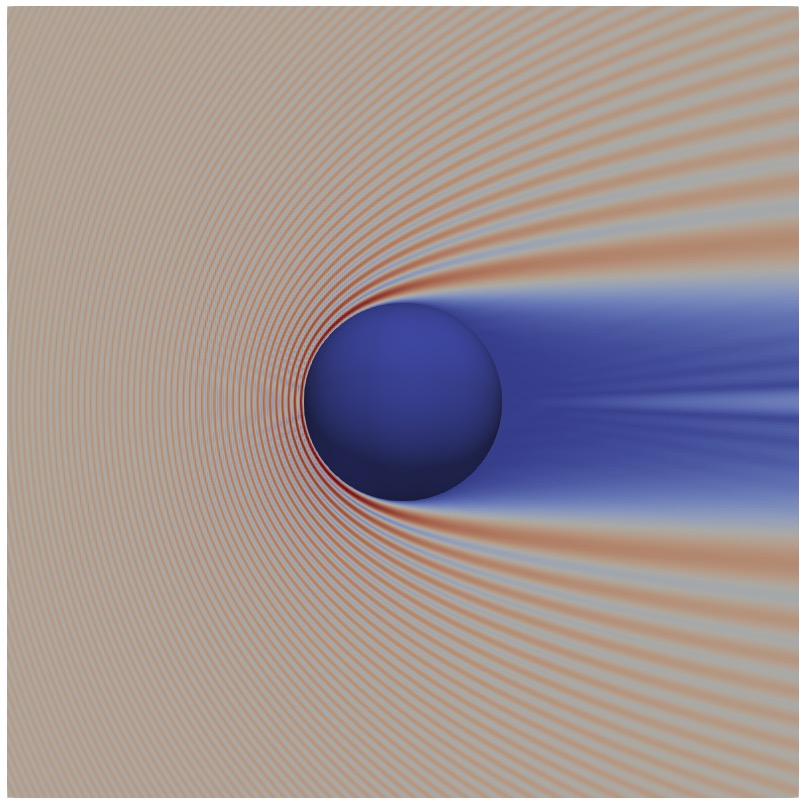
We consider the sound-soft scattering of a plane wave \(u^i(r,\theta)=e^{ikr\cos\theta}\) by the unit sphere. We choose \(\eta=k/2\) and discretize the boundary integral equation with a boundary element method with linear basis functions/planar triangles (\(p=q=1\)) and quadratic basis functions/triangles (\(p=q=2\)). We take \(k=2\pi\), solve for \(\varphi^s\), and evaluate the far-field pattern $$ u_\infty(\boldsymbol{\theta}) = \frac{1}{4\pi}\int_{\partial D} e^{-ik\boldsymbol{\theta}\cdot\boldsymbol{y}}\varphi^s(\boldsymbol{y})dS(\boldsymbol{y}), \;\; \boldsymbol{\theta}\in\mathbb{S}^2, $$ for an increasing number of triangles. We observe quartic superconvergence for quadratic elements as the mesh size \(h\to0\).
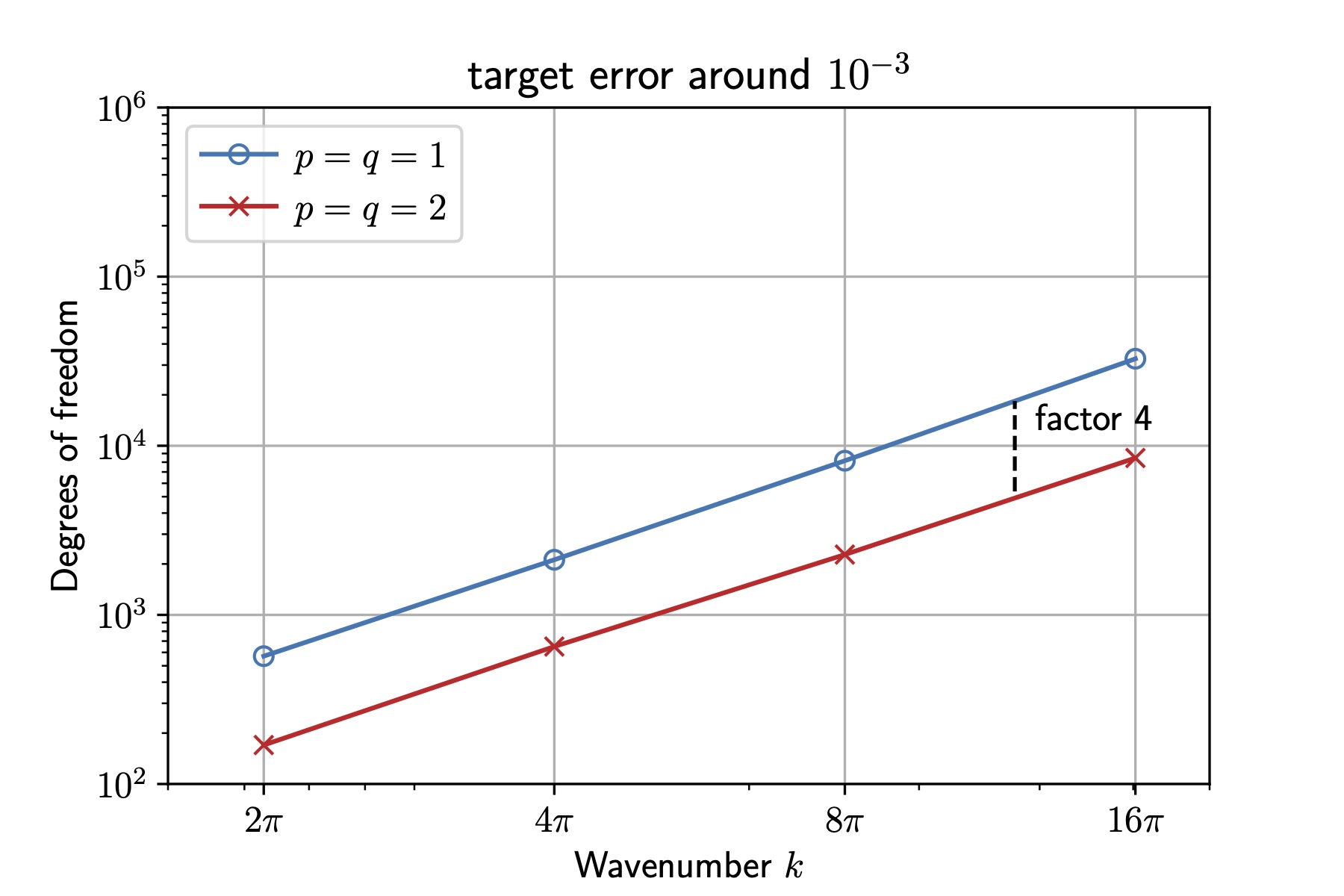
We now take \(k\in\{2\pi,4\pi,8\pi,16\pi\}\), solve for \(\varphi^s\) and seek the number of degrees of freedom needed to reach a relative error on the far-field pattern around \(10^{-3}\) for each \(k\). We observe that using quadratic elements reduces the number of degrees of freedom by a factor of about four, while also decreasing computer time by a similar factor at high frequency.
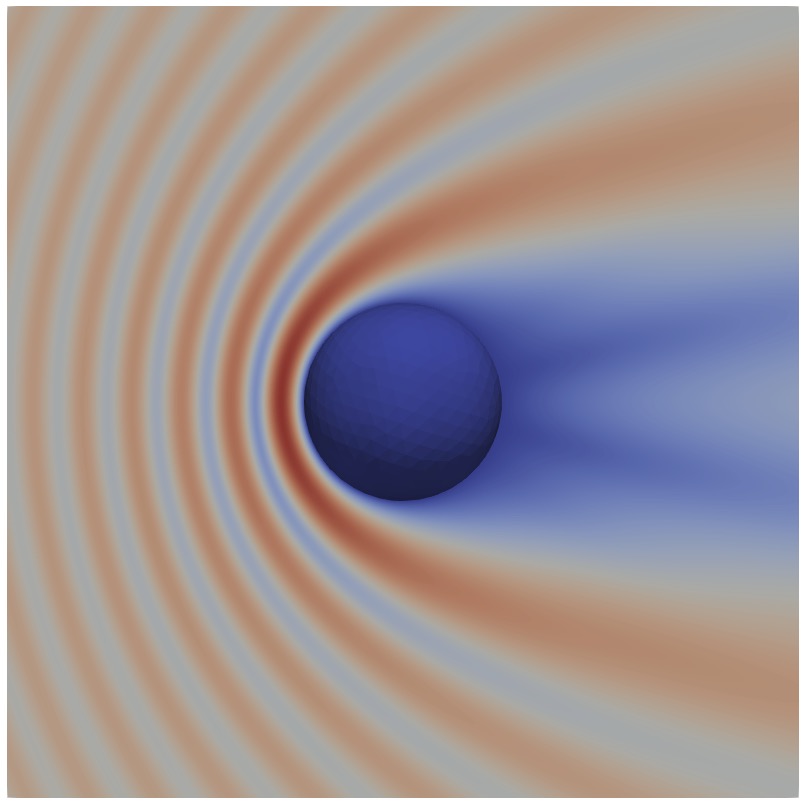
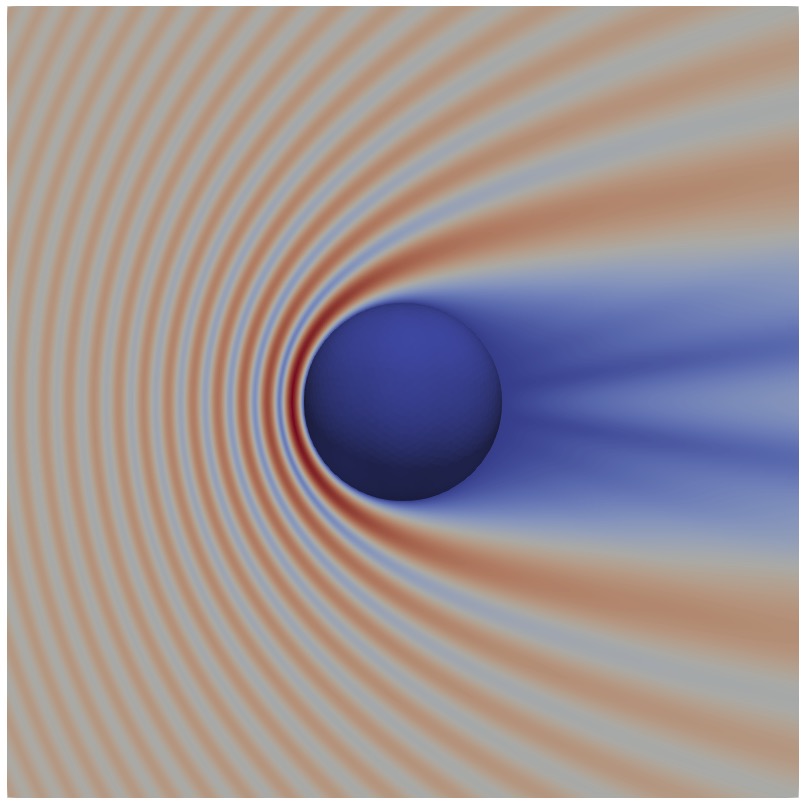
This is how the solutions look like.
Check out our paper for details!